Algebra de Boole

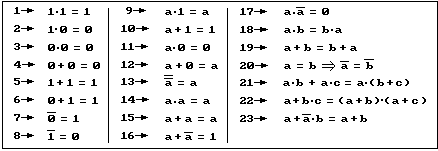
el álgebra booleana es un sistema matemático deductivo centrado en los valores cero y uno (falso y verdadero). Un operador binario " º " definido en éste juego de valores acepta un par de entradas y produce un solo valor booleano, por ejemplo, el operador booleano AND acepta dos entradas booleanas y produce una sola salida booleana.
Para cualquier sistema algebraico existen una serie de postulados iniciales, de aquí se pueden deducir reglas adicionales, teoremas y otras propiedades del sistema, el álgebra booleana a menudo emplea los siguientes postulados:

• Cerrado. El sistema booleano se considera cerrado con respecto a un operador binario si para cada par de valores booleanos se produce un solo resultado booleano.
• Conmutativo. Se dice que un operador binario " º " es conmutativo si A º B = B º A para todos los posibles valores de A y B.
• Asociativo. Se dice que un operador binario " º " es asociativo si (A º B) º C = A º (B º C) para todos los valores booleanos A, B, y C.
• Distributivo. Dos operadores binarios " º " y " % " son distributivos si A º (B % C) = (A º B) % (A º C) para todos los valores booleanos A, B, y C.
• Identidad. Un valor booleano I se dice que es un elemento de identidad

con respecto a un operador binario " º " si A º I = A.
• Inverso. Un valor booleano I es un elemento inverso con respecto a un operador booleano " º " si A º I = B, y B es diferente de A, es decir, B es el valor opuesto de A.

Para nuestros propósitos basaremos el álgebra booleana en el siguiente juego de operadores y valores:
- Los dos posibles valores en el sistema booleano son cero y uno, a menudo llamaremos a éstos valores respectivamente como falso y verdadero.
- El símbolo ·  representa la operación lógica AND. Cuando se utilicen nombres de variables de una sola letra se eliminará el símbolo ·,  por lo tanto AB representa la operación lógica AND entre las variables A y B, a esto también le llamamos el producto entre A y B.
- El símbolo "+" representa la operación lógica OR, decimos que A+B es la operación lógica OR entre A y B, también llamada la suma de A y B.
- El complemento lógico, negación ó NOT es un operador unitario, en éste texto utilizaremos el símbolo " ' " para denotar la negación lógica, por ejemplo, A' denota la operación lógica NOT de A.
- Si varios operadores diferentes aparecen en una sola expresión booleana, el resultado de la expresión depende de la procedencia de los operadores,

la cual es de mayor a menor, paréntesis, operador lógico NOT, operador lógico AND y operador lógico OR. Tanto el operador lógico AND como el OR son asociativos por la izquierda. Si dos operadores con la misma procedencia están adyacentes, entonces se evalúan de izquierda a derecha. El operador lógico NOT es asociativo por la derecha.
Utilizaremos además los siguientes postulados:

• P1 El álgebra booleana es cerrada bajo las operaciones AND, OR y NOT
• P2 El elemento de identidad con respecto a ·  es uno y con respecto a +  es cero. No existe elemento de identidad para el operador NOT
• P3 Los operadores ·   y + son conmutativos.
• P4 ·   y + son distributivos uno con respecto al otro, esto es, A· (B+C) = (A·B)+(A·C) y A+ (B·C) = (A+B) ·(A+C).
• P5 Para cada valor A existe un valor A' tal que A·A' = 0 y A+A' = 1. Éste valor es el complemento lógico de A.
• P6 ·   y + son ambos asociativos, ésto es, (AB) C = A (BC) y (A+B)+C = A+ (B+C).

                                     

Es posible probar todos los teoremas del álgebra booleana utilizando éstos postulados, además es buena idea familiarizarse con algunos de los teoremas más importantes de los cuales podemos mencionar los siguientes:

• Teorema 1: A + A = A
• Teorema 2: A · A = A
• Teorema

3: A + 0 = A
• Teorema 4: A · 1 = A
• Teorema 5: A · 0 = 0
• Teorema 6: A + 1 = 1
• Teorema 7: (A + B)' = A' · B'
• Teorema 8: (A · B)' = A' + B'
• Teorema 9: A + A · B = A
• Teorema 10: A · (A + B) = A
• Teorema 11: A + A'B = A + B
• Teorema 12: A' · (A + B') = A'B'
• Teorema 13: AB + AB' = A
• Teorema 14: (A' + B') · (A' + B) = A'
• Teorema 15: A + A' = 1
• Teorema 16: A · A' = 0
TEOREMAS

Teorema 1: El resultado de aplicar cualquiera de las tres operaciones definidas a variables del sistema booleano es otra variable del sistema y este resultado es único. Este teorema se llama Ley interna.
• Teorema 2: Ley de involución: una variable doblemente complementada es ella misma ( A ) = A.
• Teorema 3: Ley de idempotencia: A + A = A ; A · A = A.
• Teorema 4: Ley conmutativa: A + B = B + A ; A · B = B · A.
• Teorema 5: Ley asociativa (A + B) + C = A + (B + C)
(A · B) · C = A · (B · C)
• Teorema 6: Ley distributiva A ·(B + C) = (A · B) + (A · C)
A + ( B · C) = (A + B) · (A + C)
• Teorema 7: Ley de absorción A + AB = A
A · (A + B) = A
• Teorema 8: Leyes de morgan A + B = A · B
A · B = A + B
Todos estos teoremas pueden demostrarse haciendo uso de las tablas de verdad.
X + 0 = X X + 1 = 1 X +

X = 1
X · 0 = 0 X · 1 = X X · X = 0

Los teoremas siete y ocho son conocidos como Teoremas de De Morgan en honor al matemático que los descubrió.

Características:

Un álgebra de Boole es un conjunto en el que destacan las siguientes características:

1- Se han definido dos funciones binarias (que necesitan dos parámetros) que llamaremos aditiva (que representaremos por x + y) y multiplicativa (que representaremos por xy) y una función monaria (de un solo parámetro) que representaremos por x’.

2- Se han definido dos elementos (que designaremos por 0 y 1) Y 3- Tiene las siguientes propiedades:

• Conmutativa respecto a la primera función: x + y = y + x

Conmutativa respecto a la segunda función: xy = yx

Asociativa respecto a la primera función: (x + y) + z = x + (y +z)

Asociativa respecto a la segunda función: (xy)z = x(yz)

Distributiva respecto a la primera función: (x +y)z = xz + yz

Distributiva respecto a la segunda función: (xy) + z = (x + z)( y + z)

Identidad respecto a la primera función: x + 0 = x

Identidad respecto a la segunda función: x1 = x

Complemento respecto a la primera función: x + x’ = 1

Complemento respecto a la segunda función: xx’ = 0

Propiedades Del Álgebra

De Boole

1. Idempotente respecto a la primera función: x + x = x

Idempotente respecto a la segunda función: xx = x

Maximalidad del 1: x + 1 = 1

Minimalidad del 0: x0 = 0

Involución: x’‘ = x

Inmersión respecto a la primera función: x + (xy) = x

Inmersión respecto a la segunda función: x(x + y) = x

Ley de Morgan respecto a la primera función: (x + y)’ = x’y’

Ley de Morgan respecto a la segunda función: (xy)’ = x’ + y’

Función Booleana

Una función booleana es una aplicación de A x A x A x….A en A, siendo A un conjunto cuyos elementos son 0 y 1 y tiene estructura de álgebra de Boole.

Supongamos que cuatro amigos deciden ir al cine si lo quiere la mayoría. Cada uno puede votar si o no. Representemos el voto de cada uno por xi. La función devolverá sí (1) cuando el numero de votos afirmativos sea 3 y en caso contrario devolverá 0.

Si x1 vota 1, x2 vota 0, x3 vota 0 y x4 vota 1 la función booleana devolverá 0.

Producto mínimo (es el número posible de casos) es un producto en el que aparecen todas las variables o sus negaciones.